Update log
- 2020-05-12 Section2 till 2.2.1
- 2020-01-27 Introdution+section1+section 3.1
Start from a typical versual illusion(2020/01/27 update)
Since I am a student who is doing research about thermal illusion based on the existed optical illusion, I am going to describe some optical illusions from today.
I will start my work from a book which is called 新 錯視図鑑: 脳がだまされる奇妙な世界を楽しむ・解き明かす・つくりだす.
Due to limit of my spare time, I may possibily have not enough time to describe all about the illusions. I will introduce those illusions that are related to shape and brightness because these kinds of illusions are almost the most famous ones and can be transfered to some other percepts such as thermal percept. I will introduce them from from 4 basic parts
-
What is illusion?
-
Mechanism of illusion
-
Illusion of shape or size
-
Illusion of brightness
1. What is illusion?
(From wikipedia) An optical illusion (also called a visual illusion) is an illusion caused by the visual system and characterized by a visual percept that arguably appears to differ from reality. We human being observe the world, recognize the world through our eyes in our daily life. 70% of the information processed in our brain come from optical information so it is really very important for us tounderstand what we see through the eyes. On the other hand, optical illusions are not rare things for us so we also need to understand the illusions well.
A typical optical illusion may be barber’s pole.A spinning barber pole creates a visual illusion, in which the stripes appear to be traveling up or down the length of the pole, rather than around it. This illusion occurs because a bar or contour within a frame of reference provides ambiguous information about its “real” direction of movement. The actual motion of the line has many possibilities. The shape of the aperture thus tends to determine the perceived direction of motion for an otherwise identically moving contour. A vertically elongated aperture makes vertical motion dominant whereas a horizontally elongated aperture makes horizontal motion dominant. In the case of a circular or square aperture, the perceived direction of movement is usually orthogonal to the orientation of the stripes (diagonal, in this case). The perceived direction of movement relates to the termination of the line’s end points within the inside border of the occluder. The vertical aperture, for instance, has longer edges at the vertical orientation, creating a larger number of terminators unambiguously moving vertically. This stronger motion signal forces us to perceive vertical motion. Functionally, this mechanism has evolved to ensure that we perceive a moving pattern as a rigid surface moving in one direction.
However, illusions come in a wide variety; their categorization is difficult because the underlying cause is often not clear but a classification proposed by Richard Gregory is useful as an orientation. According to that, there are three main classes: physical, physiological, and cognitive illusions, and in each class there are four kinds: Ambiguities, distortions, paradoxes, and fictions. A classical example for a physical distortion would be the apparent bending of a stick half immerged in water; an example for a physiological paradox is the motion aftereffect (where, despite movement, position remains unchanged). An example for a physiological fiction is an afterimage. Three typical cognitive distortions are the Ponzo, Poggendorff, and Müller-Lyer illusion. Physical illusions are caused by the physical environment, e.g. by the optical properties of water. Physiological illusions arise in the eye or the visual pathway, e.g. from the effects of excessive stimulation of a specific receptor type. Cognitive visual illusions are the result of unconscious inferences and are perhaps those most widely known.
Pathological visual illusions arise from pathological changes in the physiological visual percept mechanisms causing the aforementioned types of illusions; they are discussed e.g. under visual hallucinations.
(atmosphere –> mechanism)
2.Mechanism of illusion
2.1 Why does illusion cannot be fixed?
The characteristic of illusion is not only seeing those things that are not fact, even though we human beings are told that ‘it’s not fact!’, it is very difficult to fix according to our sense, illusion still occurs. So here is the question: Why we cannot fix the illusion even though we know the fact?
One possibile reason is that, the optical information that is caught by retina(organization at eyes) is trasnfered to brain and processed at brain. At this time, first, the optical signals are processed in various neurons of narrow areas of retina. Then, the calculated results are transfered to the neurons of comparatively large areas of retina. At last, these information are processed and united at area that performs GLOBAL process.
At the original phase, neurons at a very large scale work independently. They are unconscious process. However, logistic process based on sense belongs to almost the final phase.
On the other hand, at the perception level, the processed results that are performed by the neurons at original phase are also reflected in our perception. In this case, at LOCAL areas of retina, process results like detecting edge of direction are transfered to perception level independentlt. These results are not necessarily united as a whole.
If this is true, those signal processing results are almost results that performed at unconscious phase. As a result, it becomes understandable that even though we are told the fact. This is an understanding of the fact that we cannot fix illusion. In this case, even we feel troubled when we face illusion, we do not need to make any effort to fix it. On the other hand, we have no way but to consider one way to adapt to the illusion.
2.2 Main theories of illusion
There are still much things that we do not know about the mechanism of illusion. However, we can still explain part of the illusions. Moreover, even we cannot explain all about some illusion, we can estimate the possible mechanism of some illusion. Here I will introduce main theories about illusions.
2.2.1 Optical illusion created by movement of lines due to smoothing
Here I would like to introduce the theory(Fermuller and Malm,2004) that explains the many illusions of transformated shapes. In this theory, when the figure is caught at retina, due to the limitaion of resolution of retina, error called smoothing occurs. Smoothing is the reason that causes the gap of location of the lines.
Smoothing is an operation that replaces brightness of each point by an average value.
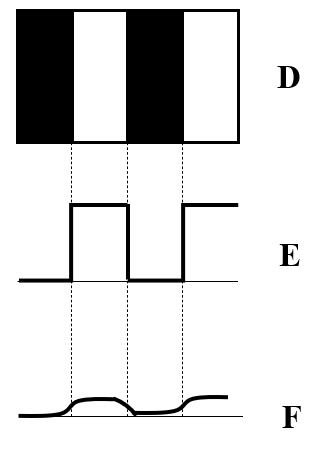As the figure shows above, edge that devides the black block and white block in D, can be shown as the graph in E. Graph E show the brightness value spatially. It looks like a step. When smoothing is performed, step line in graph E becomes gentle. This process is called smoothing. Notice that, where it was black becomes white, and where it was white becomes black at some areas. However, the location of edge does not change. So we can say that smoothing does not change the location of edge.
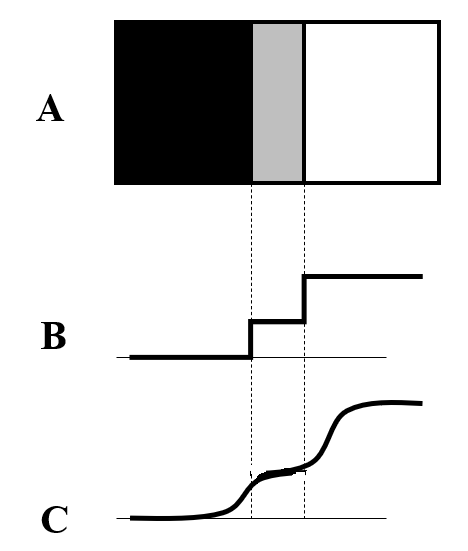As the figure shows above, as shown in A and B, when there is a narrow gray line between the white and black regions, when smoothing is performed, white and black erode into gray as shown in C, and the gray line becomes It becomes thin. That is, due to the smoothing, the right side of the gray line moves to the left and the left side moves to the right.
In visual system, there is a theory that expalains the edge detection mechanism. It uses DOG(difference of two Gaussians) filter. This filter is a bandpass filter, which fits the spatial frequency characteristic of visual cells. The filter can be stated as below:
$r\left ( x,y \right )=\frac{1}{2\pi \sigma _{e}^{2}}exp(-\frac{x^{2}+y^{2}}{2\sigma _{e}^{2}})-\frac{1}{2\pi \sigma _{i}^{2}}exp(-\frac{x^{2}+y^{2}}{2\sigma _{i}^{2}})$
Where $\sigma {e}$ and $\sigma _{i}$ describe spatial frequency of human sensation. The frequency response can be described by its Fourier transform$R(f{x},f_{y})$:
$R(f_{x},f_{y})=exp{-\frac{(2\pi\sigma {e})^{2}}{2}(f{x}^{2}+f_{y}^{2})} - exp{-\frac{(2\pi\sigma {i})^{2}}{2}(f{x}^{2}+f_{y}^{2})}$
Where $f_{x}$ and $f_{y}$ are the spatial frequency along x-axis and y-axis. The perceived stimuli b (x, y) can be calculated by the formula in the figure, where r (x, y) is the function that represents the DOG filter, and l (x, y) is the stimuli distribution of the pattern:
$b(x,y)=\iint r(X-x,Y-y)l(X,Y)dXdY$
2.2.2 Depth-guided illusion
2.2.3 Optical illusion caused by comparison of nearby objects
3.Illusion of shape or size
3.1Cafe Wall Illusin
The Café Wall illusion is an optical illusion first described by Dr. Richard Gregory. He observed this curious effect on the wall tiles of a cafe at the bottom of St. Michael’s Hill in Bristol.
This illusion is one in which parallel horizontal lines appear to bend.
To create this illusion, light-colored and dark-colored bricks are alternately staggered. It is important to apply mortar (gray in the image) around the bricks. The ideal color for this mortar is a color between the shades of the bricks.
The Café Wall illusion is not well understood. The perception of oblique lines is due to the interaction of neurons in the brain. Different types of neurons respond to the perception of dark and light colors, and different parts of the grout line are darkened or lightened on the retina because of the placement of dark and light tiles. This effect may involve interactions between neurons that encode orientation in the visual cortex. However, it is unclear whether this effect is due to an inhibitory mechanism or whether there is a kind of computational filter that acts on inputs from cells operating at different spatial frequencies.
The Café Wall illusion has helped neuropsychologists study how visual information is processed by the brain. The illusion has also been applied to graphic design, art, and architecture.
source: http://nekomosyakushimo.hatenablog.com/entry/2017/09/06/012510
python code
#coding:utf-8
from __future__ import division
from __future__ import unicode_literals
from numpy import array
from PIL import Image, ImageDraw
#黒の四角の位置情報
black1 = array(range(5)) * 120 + 30
#描画オブジェクトとか
image = Image.new("RGB", (620,123), color=(255,255,255))
draw = ImageDraw.Draw(image)
for i in range(5): #上段の四角形を描く
draw.rectangle(((black1[i],0),(black1[i]+60,60)), outline = None, fill = (0,0,0))
for j in range(5): #下段の四角形を描く
draw.rectangle(((black1[j]+30,63),(black1[j]+90,123)), outline = None, fill = (0,0,0))
draw.line([(0,61),(620,61)], width = 2, fill = (128,128,128)) #真ん中の灰色の線
image.save("cafe.png")
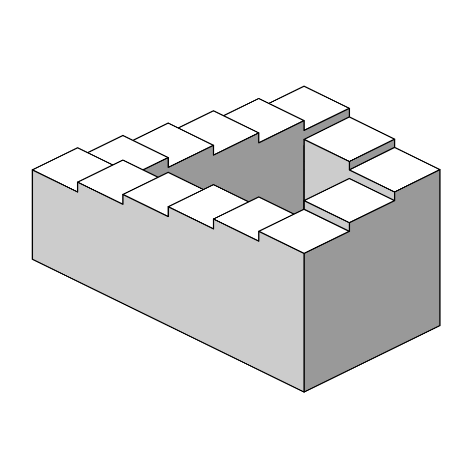
3.2Penrose Stairs
The Penrose Stairs Figure was created by Lionel Sharples Penrose (1898 -1972), a British psychiatrist, geneticist, and mathematician, and his son Sir Roger Penrose (1931 -), a British mathematician, physicist and philosopher of science. It was first published in the British Journal of Psychology in 1958.
The Penrose Stairs is an impossible figure (or impossible object or undecidable figure): it depicts an object which could not possibly exist. It is impossible for the Penrose Stairs to exist because in order for it to exist rules of Euclidean geometry would have to be violated. For example, if one were to complete a circuit of the stairs, one would end up back at the same level that one began, even though each flight of the stairs continuously rise (or fall, depending on the direction of travel). It is one of many types of impossible figures which you can search for in the Illusions Index.
Philosophers have also been interested in what impossible figures can tell us about the nature of the content of experience. For example, impossible figures seem to provide examples of experiences with content that is contradictory, which some philosophers have taken to challenge the claim that perceptual states are belief-like (Macpherson 2010). They also prove problematic for sense-data accounts of perception that posit that corresponding to every experience that we have there are mental objects that we are aware of that have the properties that the objects that our experiences tell us they do. They problem is that sense-data would have to be impossible objects. But, surely, impossible objects can’t exist!
4.Illusion of brightness
5.Instantaneous view condition, relay prompt condition
If one does not care about the involvement of Bloch’s law, etc., it has been reported that the same amount of illusion as usual was obtained after only 2 ms of presentation. If the illusion is recognized, the illusion is valid. However, there are some reports of a slight increase in the amount of illusion during a short presentation time (50-100 ms), and some reports of a regular decrease in the amount of illusion. However, there is a slight increase in the amount of illusion during a short presentation time (50-100 ms), while there is a regular decrease in the amount of illusion during a short presentation time (50-100 ms).
