I made a latex math editor for local use. so I do not have to use the editor online.
vanilla version
"""
https://github.com/MorvanZhou/tutorials/blob/master/tkinterTUT/tk3_entry_text.py
https://stackoverflow.com/questions/44443270/use-latex-symbols-in-sympy-expressions
"""
import tkinter as tk
import sympy as sym
import sympy.printing as printing
window = tk.Tk()
window.title('my window')
window.geometry('200x200')
# e = tk.Entry(window, show="*")
#e = tk.Entry(window, show="1")
e = tk.Entry(window, bd=10)
e.pack()
def transform():
var = e.get()
string = sym.symbols(var)
t.insert('insert', printing.latex(string))
b1 = tk.Button(window, text='transform', width=15,
height=2, command=transform)
b1.pack()
t = tk.Text(window, height=3)
t.pack()
window.mainloop()
version 1.0
"""
https://github.com/MorvanZhou/tutorials/blob/master/tkinterTUT/tk3_entry_text.py
https://stackoverflow.com/questions/44443270/use-latex-symbols-in-sympy-expressions
"""
import tkinter as tk
import sympy as sym
import sympy.printing as printing
window = tk.Tk()
window.title('my window')
window.geometry('540x400')
large_font = ('Verdana',20)
e = tk.Entry(window, bd=2,width=50,font=large_font)
e.pack()
def transform():
var = e.get()
string = sym.symbols(var)
t.insert('insert', printing.latex(string))
b1 = tk.Button(window, text='transform', width=50,
height=2, command=transform)
b1.pack()
t = tk.Text(window, height=5)
t.pack()
def alpha():
e.insert('insert', 'α')
def Beta():
e.insert('insert', 'β')
def Gamma():
e.insert('insert', 'γ')
def Delta():
e.insert('insert', 'δ')
def Epsilon():
e.insert('insert', 'ε')
def Theta():
e.insert('insert', 'θ')
def Kappa():
e.insert('insert', 'κ')
def Lambda():
e.insert('insert', 'λ')
def Mu():
e.insert('insert', 'μ')
def Xi():
e.insert('insert', 'ξ')
def Pi():
e.insert('insert', 'π')
def Rho():
e.insert('insert', 'ρ')
def Sigma():
e.insert('insert', 'σ')
def Tau():
e.insert('insert', 'τ')
def Phi():
e.insert('insert', 'φ')
def Chi():
e.insert('insert', 'χ')
def Psi():
e.insert('insert', 'ψ')
def Omega():
e.insert('insert', 'ω')
wid=30
hei=30
# Greek
btn_alpha = tk.Button(window,text = 'α',bd = 0.5,command = alpha)
btn_alpha.place(x = 0,y = 285,width = wid,height = hei)
btn_alpha = tk.Button(window,text = 'β',bd = 0.5,command = Beta)
btn_alpha.place(x = 0+wid*1,y = 285,width = wid,height = hei)
btn_alpha = tk.Button(window,text = 'γ',bd = 0.5,command = Gamma)
btn_alpha.place(x = 0+wid*2,y = 285,width = wid,height = hei)
btn_alpha = tk.Button(window,text = 'δ',bd = 0.5,command = Delta)
btn_alpha.place(x = 0+wid*3,y = 285,width = wid,height = hei)
btn_alpha = tk.Button(window,text = 'ε',bd = 0.5,command = Epsilon)
btn_alpha.place(x = 0+wid*4,y = 285,width = wid,height = hei)
btn_alpha = tk.Button(window,text = 'θ',bd = 0.5,command = Theta)
btn_alpha.place(x = 0+wid*5,y = 285,width = wid,height = hei)
btn_alpha = tk.Button(window,text = 'κ',bd = 0.5,command = Kappa)
btn_alpha.place(x = 0+wid*6,y = 285,width = wid,height = hei)
btn_alpha = tk.Button(window,text = 'λ',bd = 0.5,command = Lambda)
btn_alpha.place(x = 0+wid*7,y = 285,width = wid,height = hei)
btn_alpha = tk.Button(window,text = 'μ',bd = 0.5,command = Mu)
btn_alpha.place(x = 0+wid*8,y = 285,width = wid,height = hei)
btn_alpha = tk.Button(window,text = 'ξ',bd = 0.5,command = Xi)
btn_alpha.place(x = 0+wid*0,y = 285+hei*1,width = wid,height = hei)
btn_alpha = tk.Button(window,text = 'π',bd = 0.5,command = Pi)
btn_alpha.place(x = 0+wid*1,y = 285+hei*1,width = wid,height = hei)
btn_alpha = tk.Button(window,text = 'ρ',bd = 0.5,command = Rho)
btn_alpha.place(x = 0+wid*2,y = 285+hei*1,width = wid,height = hei)
btn_alpha = tk.Button(window,text = 'σ',bd = 0.5,command = Sigma)
btn_alpha.place(x = 0+wid*3,y = 285+hei*1,width = wid,height = hei)
btn_alpha = tk.Button(window,text = 'τ',bd = 0.5,command = Tau)
btn_alpha.place(x = 0+wid*4,y = 285+hei*1,width = wid,height = hei)
btn_alpha = tk.Button(window,text = 'φ',bd = 0.5,command = Phi)
btn_alpha.place(x = 0+wid*5,y = 285+hei*1,width = wid,height = hei)
btn_alpha = tk.Button(window,text = 'χ',bd = 0.5,command = Chi)
btn_alpha.place(x = 0+wid*6,y = 285+hei*1,width = wid,height = hei)
btn_alpha = tk.Button(window,text = 'ψ',bd = 0.5,command = Psi)
btn_alpha.place(x = 0+wid*7,y = 285+hei*1,width = wid,height = hei)
btn_alpha = tk.Button(window,text = 'ω',bd = 0.5,command = Omega)
btn_alpha.place(x = 0+wid*8,y = 285+hei*1,width = wid,height = hei)
# function
def xa():
e.insert('insert', '^{U}')
def xab():
e.insert('insert', '_{L}^{U}')
def ppx():
e.insert('insert', ' \frac{\partial ?}{\partial x}')
def p2px2():
e.insert('insert', ' \frac{\partial^2 ?}{\partial x^2}')
def ddx():
e.insert('insert', ' \frac{\mathrm{d} ?}{\mathrm{d} x}')
def inte():
e.insert('insert', '\int ?')
def inteab():
e.insert('insert', '\int_{L}^{U}')
btn_xa = tk.Button(window,text = 'x^(a)',bd = 0.5,command = xa)
btn_xa.place(x = 0+wid*10,y = 285,width = wid,height = hei)
btn_xab = tk.Button(window,text = 'x_(a)^(b)',bd = 0.5,command = xab)
btn_xab.place(x = 0+wid*11,y = 285,width = wid*2,height = hei)
btn_ppx = tk.Button(window,text = 'p/px',bd = 0.5,command = ppx)
btn_ppx.place(x = 0+wid*13,y = 285,width = wid*2,height = hei)
btn_ddx = tk.Button(window,text = 'd/dx',bd = 0.5,command = ddx)
btn_ddx.place(x = 0+wid*15,y = 285,width = wid,height = hei)
btn_inte = tk.Button(window,text = 'integral',bd = 0.5,command = inte)
btn_inte.place(x = 0+wid*16,y = 285,width = wid*2,height = hei)
btn_inteab = tk.Button(window,text = 'integralab',bd = 0.5,command = inteab)
btn_inteab.place(x = 0+wid*10,y = 285+hei,width = wid*2,height = hei)
window.mainloop()
version 2.0
""" https://stackoverflow.com/questions/36636185/is-it-possible-for-python-to-display-latex-in-real-time-in-a-text-box """
import matplotlib
import matplotlib.pyplot as plt
from matplotlib.backends.backend_tkagg import FigureCanvasTkAgg
matplotlib.use('TkAgg')
from Tkinter import *
from ttk import *
def graph(text):
tmptext = entry.get()
tmptext = "$"+tmptext+"$"
ax.clear()
ax.text(0.2, 0.6, tmptext, fontsize = 50)
canvas.draw()
root = Tk()
mainframe = Frame(root)
mainframe.pack()
text = StringVar()
entry = Entry(mainframe, width=100, textvariable=text)
entry.pack()
label = Label(mainframe)
label.pack()
fig = matplotlib.figure.Figure(figsize=(4, 2), dpi=200)
ax = fig.add_subplot(111)
canvas = FigureCanvasTkAgg(fig, master=label)
canvas.get_tk_widget().pack(side=TOP, fill=BOTH, expand=1)
canvas._tkcanvas.pack(side=TOP, fill=BOTH, expand=1)
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
#Greek
def alpha():
entry.insert('insert', 'α')
def Beta():
entry.insert('insert', 'β')
def Gamma():
entry.insert('insert', 'γ')
def Delta():
entry.insert('insert', 'δ')
def Epsilon():
entry.insert('insert', 'ε')
def Theta():
entry.insert('insert', 'θ')
def Kappa():
entry.insert('insert', 'κ')
def Lambda():
entry.insert('insert', 'λ')
def Mu():
entry.insert('insert', 'μ')
def Xi():
entry.insert('insert', 'ξ')
def Pi():
entry.insert('insert', 'π')
def Rho():
entry.insert('insert', 'ρ')
def Sigma():
entry.insert('insert', 'σ')
def Tau():
entry.insert('insert', 'τ')
def Phi():
entry.insert('insert', 'φ')
def Chi():
entry.insert('insert', 'χ')
def Psi():
entry.insert('insert', 'ψ')
def Omega():
entry.insert('insert', 'ω')
wid=30
hei=30
# Greek
btn_alpha = Button(root,text = 'α',command = alpha)
btn_alpha.place(x = 0,y = 350,width = wid,height = hei)
btn_alpha = Button(root,text = 'β',command = Beta)
btn_alpha.place(x = 0+wid*1,y = 350,width = wid,height = hei)
btn_alpha = Button(root,text = 'γ',command = Gamma)
btn_alpha.place(x = 0+wid*2,y = 350,width = wid,height = hei)
btn_alpha = Button(root,text = 'δ',command = Delta)
btn_alpha.place(x = 0+wid*3,y = 350,width = wid,height = hei)
btn_alpha = Button(root,text = 'ε',command = Epsilon)
btn_alpha.place(x = 0+wid*4,y = 350,width = wid,height = hei)
btn_alpha = Button(root,text = 'θ',command = Theta)
btn_alpha.place(x = 0+wid*5,y = 350,width = wid,height = hei)
btn_alpha = Button(root,text = 'κ',command = Kappa)
btn_alpha.place(x = 0+wid*6,y = 350,width = wid,height = hei)
btn_alpha = Button(root,text = 'λ',command = Lambda)
btn_alpha.place(x = 0+wid*7,y = 350,width = wid,height = hei)
btn_alpha = Button(root,text = 'μ',command = Mu)
btn_alpha.place(x = 0+wid*8,y = 350,width = wid,height = hei)
btn_alpha = Button(root,text = 'ξ',command = Xi)
btn_alpha.place(x = 0+wid*0,y = 350+hei*1,width = wid,height = hei)
btn_alpha = Button(root,text = 'π',command = Pi)
btn_alpha.place(x = 0+wid*1,y = 350+hei*1,width = wid,height = hei)
btn_alpha = Button(root,text = 'ρ',command = Rho)
btn_alpha.place(x = 0+wid*2,y = 350+hei*1,width = wid,height = hei)
btn_alpha = Button(root,text = 'σ',command = Sigma)
btn_alpha.place(x = 0+wid*3,y = 350+hei*1,width = wid,height = hei)
btn_alpha = Button(root,text = 'τ',command = Tau)
btn_alpha.place(x = 0+wid*4,y = 350+hei*1,width = wid,height = hei)
btn_alpha = Button(root,text = 'φ',command = Phi)
btn_alpha.place(x = 0+wid*5,y = 350+hei*1,width = wid,height = hei)
btn_alpha = Button(root,text = 'χ',command = Chi)
btn_alpha.place(x = 0+wid*6,y = 350+hei*1,width = wid,height = hei)
btn_alpha = Button(root,text = 'ψ',command = Psi)
btn_alpha.place(x = 0+wid*7,y = 350+hei*1,width = wid,height = hei)
btn_alpha = Button(root,text = 'ω',command = Omega)
btn_alpha.place(x = 0+wid*8,y = 350+hei*1,width = wid,height = hei)
# function
def xa():
entry.insert('insert', '^{U}')
def xab():
entry.insert('insert', '_{L}^{U}')
def ppx():
entry.insert('insert', ' \frac{\partial ?}{\partial x}')
def p2px2():
entry.insert('insert', ' \frac{\partial^2 ?}{\partial x^2}')
def ddx():
entry.insert('insert', ' \frac{\mathrm{d} ?}{\mathrm{d} x}')
def inte():
entry.insert('insert', '\int ?')
def inteab():
entry.insert('insert', '\int_{L}^{U}')
btn_xa = Button(root,text = 'x^(a)',command = xa)
btn_xa.place(x = 0+wid*10,y = 350,width = wid,height = hei)
btn_xab = Button(root,text = 'x_(a)^(b)',command = xab)
btn_xab.place(x = 0+wid*11,y = 350,width = wid*2,height = hei)
btn_ppx = Button(root,text = 'p/px',command = ppx)
btn_ppx.place(x = 0+wid*13,y = 350,width = wid*2,height = hei)
btn_ddx = Button(root,text = 'd/dx',command = ddx)
btn_ddx.place(x = 0+wid*15,y = 350,width = wid,height = hei)
btn_inte = Button(root,text = 'integral',command = inte)
btn_inte.place(x = 0+wid*16,y = 350,width = wid*2,height = hei)
btn_inteab = Button(root,text = 'integralab',command = inteab)
btn_inteab.place(x = 0+wid*10,y = 350+hei,width = wid*2,height = hei)
root.bind('<Motion>', graph)
root.mainloop()
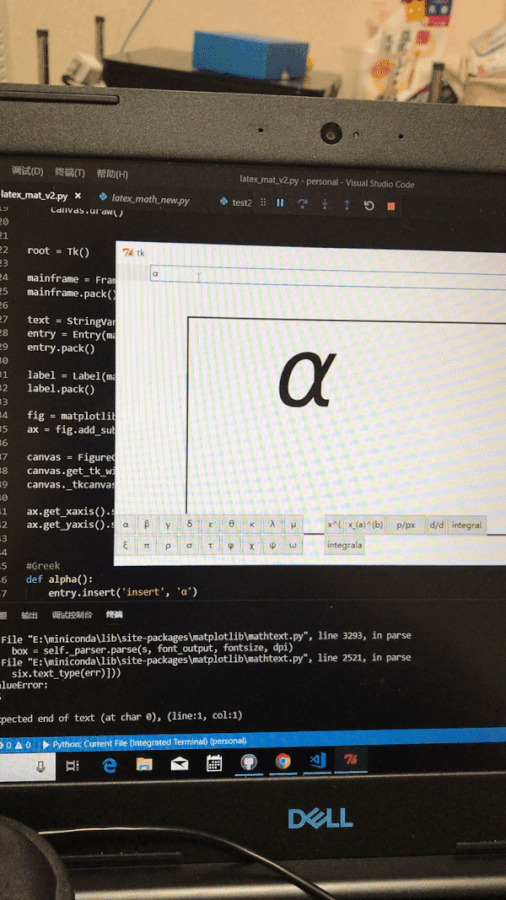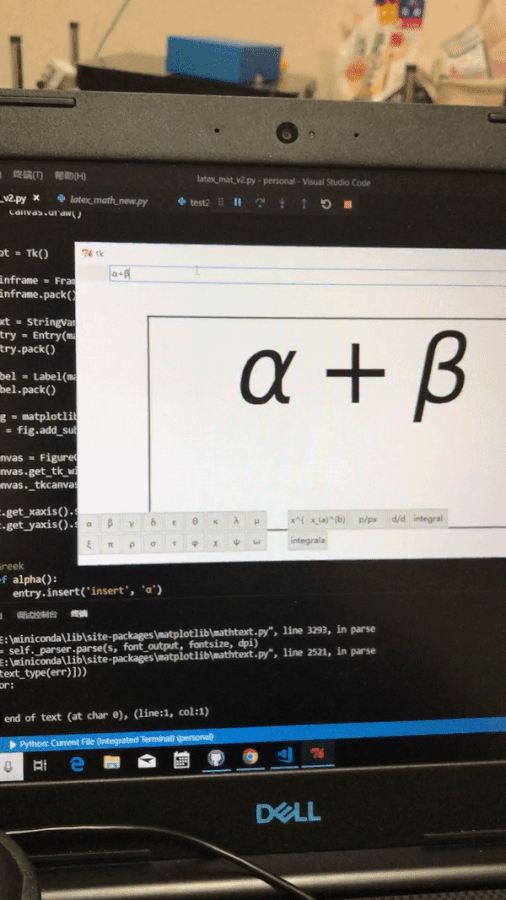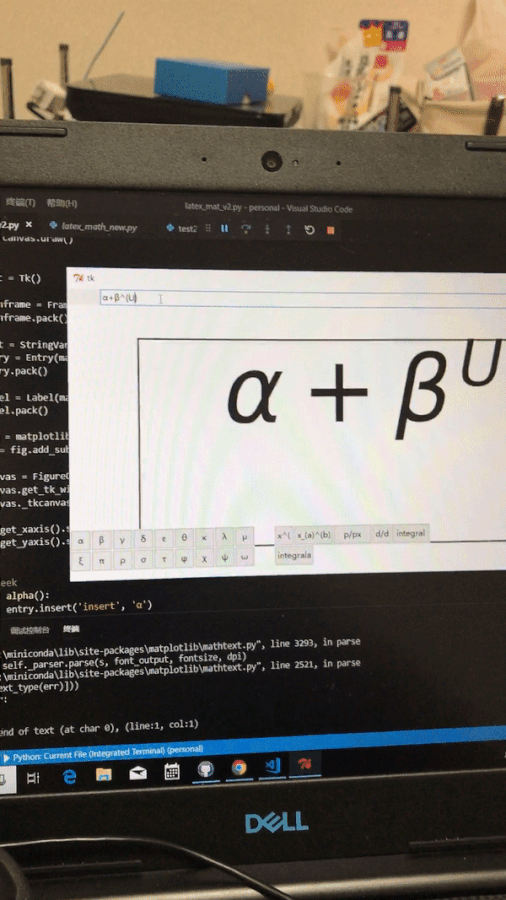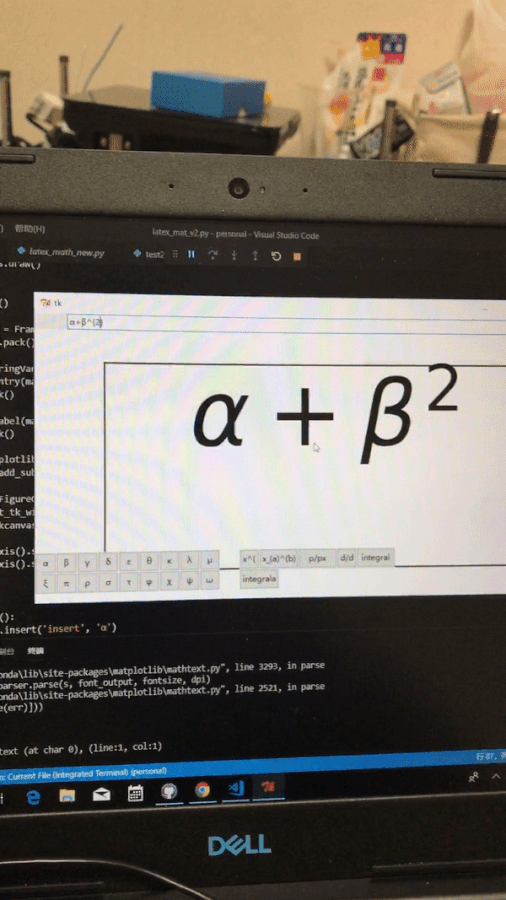
VIDEO
- https://youtu.be/H-vQI-_Hvik
2019-03-16 updated
bug fixed
ValueError:
$$$$
^
Expected end of text (at char 0), (line:1, col:1)

